Understanding Support Vector Machines

Understanding Support Vector Machines: A Deep Dive into SVMs

Support Vector Machines (SVM) are a cornerstone of machine learning, providing a powerful tool for data classification. Despite their apparent complexity, the principles behind SVM can be understood with a solid grasp of the underlying mathematics. In this blog post, we'll explore the key concepts of SVM, including how they work and their application in solving real-world problems.

What is a Support Vector Machine?

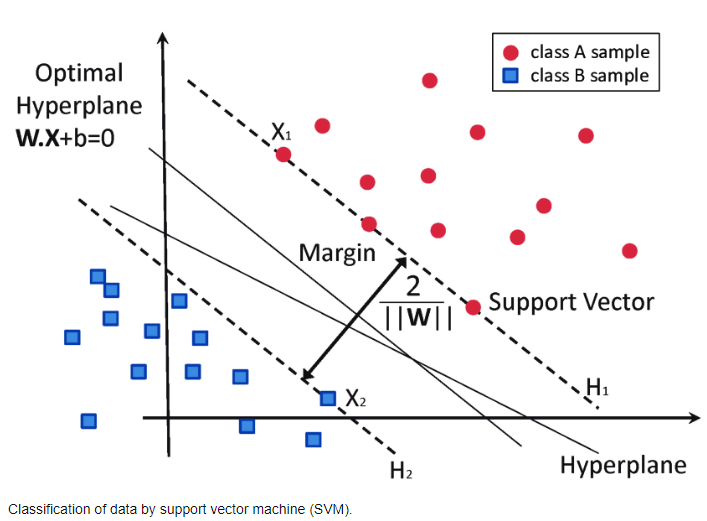
A Support Vector Machine is a supervised machine learning algorithm primarily used for classification tasks. However, with appropriate modifications, it can also handle regression problems. At its core, SVM seeks to find the best separating hyperplane that divides data points from different classes in the feature space.

The Mathematics of SVM

To understand SVM, consider a dataset with two classes, where we aim to find a decision boundary (a hyperplane in higher dimensions) that best separates the classes. This boundary is chosen to maximize the margin between the closest points of the classes, which are known as support vectors.

Linear SVM

The equation for a hyperplane in an n-dimensional space is given by:

\[ \mathbf{w} \cdot \mathbf{x} - b = 0 \]

Where:

\(\mathbf{w}\) is the weight vector perpendicular to the hyperplane.
\(\mathbf{x}\) is the feature vector.
\(b\) is the bias.

The objective is to find \(\mathbf{w}\) and \(b\) such that the margin between the two classes is maximized while keeping the classes separated. This can be formulated as:

\[ \text{Minimize } \frac{1}{2} \| \mathbf{w} \|^2 \]

\[ \text{Subject to } y_i (\mathbf{w} \cdot \mathbf{x}_i - b) \geq 1, \text{ for all } i \]

Here, \(y_i\) represents the class label of each data point, which can be either +1 or -1.

Kernel Trick

For non-linearly separable data, SVM can be extended using the kernel trick. Instead of a linear function, SVM uses a kernel function to transform the data into a higher-dimensional space where a hyperplane can effectively separate the classes.

Commonly used kernel functions include:

Polynomial: \( (x \cdot x')^d \)
Radial Basis Function (RBF): \( \exp(-\gamma \|x - x'\|^2) \)
Sigmoid: \( \tanh(\alpha x \cdot x' + c) \)

SVM in Practice

In practical applications, SVMs are used for a variety of tasks such as:

Image classification
Speech recognition
Text categorization

The effectiveness of SVM in these domains often comes from its ability to handle high-dimensional data and its robustness against overfitting, especially in cases where the number of dimensions exceeds the number of samples.

Conclusion

Support Vector Machines represent a robust method for classification, capable of handling both linear and complex non-linear relationships in data. By strategically using the kernel trick, SVMs can extend their reach to more complex scenarios, making them a versatile tool in the machine learning arsenal.

For anyone looking to dive deeper into machine learning, gaining a thorough understanding of SVM and its applications can provide a strong foundation for both theory and practical implementation in various domains.